　非線形回帰分析　-　07

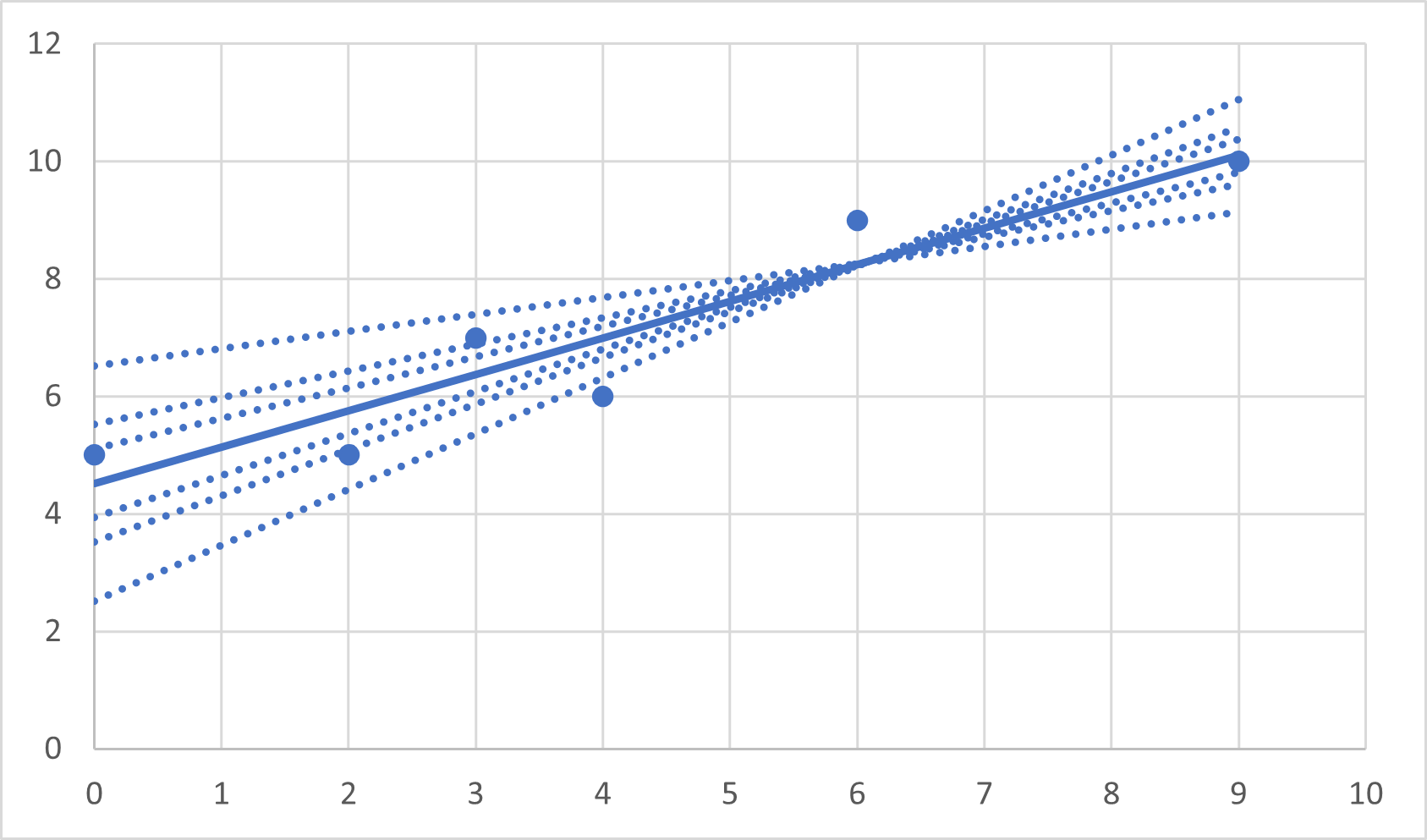
線形回帰のパラメータの推定

切片，a₂，をシフト

具体的な値は，参考にしたサイトの値を使わさせていただきます．

a₀			2.52	3.52	3.9384	4.52	5.1016	5.52	6.52
δ			-2	-1	-0.58158	0	0.58157	1	2
a₁			0.949	0.784	0.716	0.62	0.524	0.456	0.291

i	x	y		\( \hat{y} \)
1	0	5	2.52	3.52	3.938	4.52	5.101	5.52	6.52
2	2	5	4.417	5.088	5.369	5.76	6.150	6.431	7.102
3	3	7	5.366	5.873	6.085	6.38	6.674	6.886	7.393
4	4	6	6.315	6.657	6.800	7.00	7.199	7.342	7.684
5	6	9	8.212	8.226	8.232	8.24	8.247	8.253	8.267
6	9	10	11.058	10.579	10.378	10.1	9.821	9.62	9.141

S (\(y_i - \hat{y} \)の平方和)			10.999	4.835	3.475	2.78 (Se)	3.475	4.835	10.999
dS (Seとの差分）			8.219	2.055	0.695	0	0.695	2.055	8.219

切片を変えて傾きを近似すると，このようなグラフを得ることができます．

ここで，S，Se，は，

・残差平方和

推定値からの残差

\(\Large \displaystyle Se = \sum_{i=1}^{n} \left( y_i -\hat{a_0} - \hat{a_1} x_i \right)^2 \)

a₀をシフトさせたときの，推定値からの残差

\(\Large \displaystyle S = \sum_{i=1}^{n} \left( y_i -a_0 - \hat{a_1} x_i \right)^2 \)

であり，傾きの値a₀を，δ，だけシフトさせて，固定し，その際のa₁の推定値をソルバーで推定しました．

a₀の標準誤差も加えてあります．

dS，を見ていただけるとわかるように，推定値，Seが一番小さく，左右対称に増加していることがわかります．

グラフ化すると，

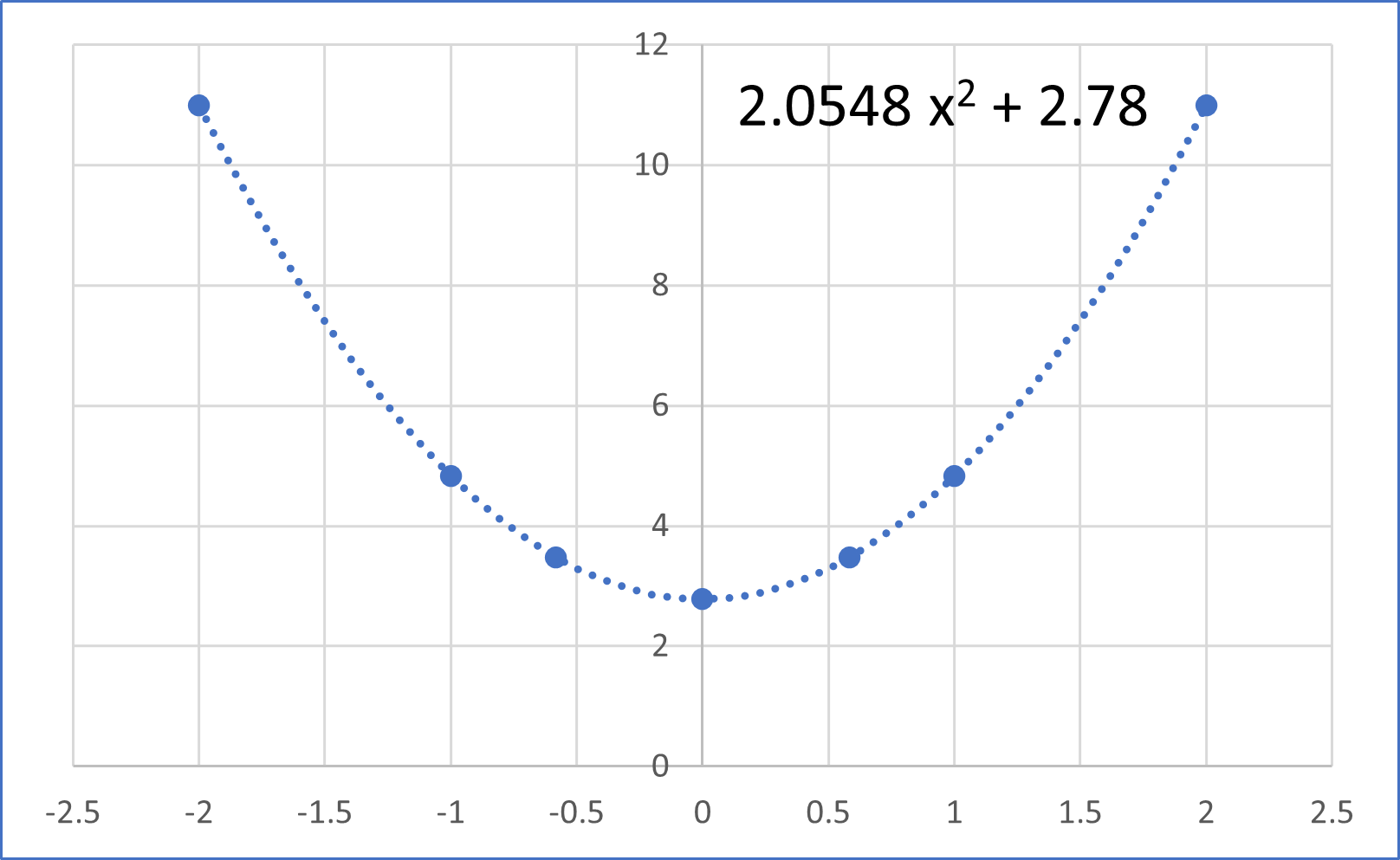
のように，二乗+定数できれいに近似できます．

ここで，分散値は，

・分散

\(\Large \displaystyle Ve = \frac{1}{n-2} \sum_{i=1}^{n} \left(y_i -\hat{a_0} - \hat{a_1} x_i \right)^2 = \frac{Se}{n-2} = \frac{2.78}{6-2} = 0.695 \)

であり（a₀，a₁，の二つのパラメータが2つあるので，自由度は，n-2），平均値の議論では，

\(\Large \displaystyle S_{SE} = Se + Ve \)

となり，当てはまりの悪さ，S，がSe + Ve，の場合のδが，標準誤差，SE，となるので，ちょうどa₀のシフトが回帰分析で計算した標準誤差，±0.58157，の時に，Se+Ve，となります．

さて，実際にパラメータをシフトさせて残差平方和を求め，その結果が”二乗+定数”，となり，平均値の場合と同様の結果となりました．

次ページは，線形回帰の場合，切片，a2，をシフト，したらどのような計算式になるのか？を考えていきましょう．

非線形回帰分析 - 07

　非線形回帰分析　-　07